![]() (1)
(1)
![]() (1)
(1)
Where ![]() - tensor describing a spin-orbit interaction;
- tensor describing a spin-orbit interaction; ![]() - tensor of decomposition in a zero field;
- tensor of decomposition in a zero field; ![]() - tensor of a hyperfine interaction.
- tensor of a hyperfine interaction.
The
tensor of decomposition in a zero field gives magnetic interaction of two
lone electrons of a pair: [3]:
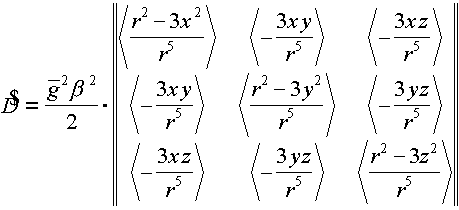 (2)
(2)
Where
the brackets < > designates an average of elements of a tensor on all
possible positional relationships of two lone electrons of a pair, ![]() - g-factor of a free electron,
- g-factor of a free electron, ![]() - electronic magneton of the Bohr. In a system of main axises the tensor
has diagonal an aspect. Through principal values of a tensor the parameters
of decomposition in a zero field D and E are:
- electronic magneton of the Bohr. In a system of main axises the tensor
has diagonal an aspect. Through principal values of a tensor the parameters
of decomposition in a zero field D and E are:
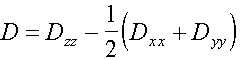 ,
(3)
,
(3)
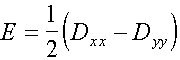 ,
(4)
,
(4)
Where ![]() - greatest modulo principal value [4].
- greatest modulo principal value [4].
ïÇÒÁÎÉÞÅÍÓÑ
in the beginning by reviewing of the first two terms of a Hamiltonian (1).
Using magnitudes D and å it is possible to present square-part on a spin
a term ![]() As [5]:
As [5]:
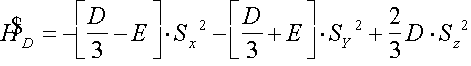 ,
(5)
,
(5)
Where x, y, z - principal coordinate axises. A complete Hamiltonian we shall receive by adding a Zeeman energy:
![]() .
(6)
.
(6)
Where ![]() - external magnetic field [5]. Generally speaking,
- external magnetic field [5]. Generally speaking, ![]() Is not equal
Is not equal ![]() - to the g-factor
of a mobile electron, that will be taken into account below.
- to the g-factor
of a mobile electron, that will be taken into account below.
The matrix of a Hamiltonian (6) in relation to basis functions Y = | j, M> of a system S = 1 (M = + 1, 0, -1) has an aspect:
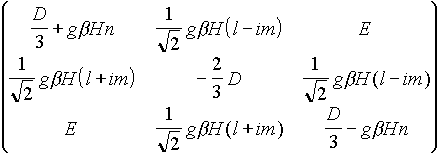 (7)
(7)
Where l, m, n - direction cosines of an external field in relation to magnetic axeses fixed in a triplet [5].
The
magnetic axeses are defined as a frame, in which Hamiltonian of magnetic
dipole - dipole interaction expresses with the help of the formula (5),
that is without crossbar products of a type SxSy, when the basis functions
are quantized along one of these axeses. Such gang of axeses always exists
[6]. They can be defined in view of a symmetry of a molecule. For example
in a triplet of Naftalen one axes is perpendicular to plane of a molecule,
second and third lays along a short symmetry axis in a plane of a molecule,
- along long [5]. In case of a low symmetry the definition of axeses direction
in relation to molecular geometry is not so obvious, but can be defined
experimentally [7].
The
eigenvalues and eigenfunctions for (7) are easily gained, when the field
î is guided along one of principal axises [8].
For
example, if î || z, levels of an energy and the spin part of wave functions
is
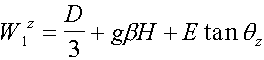 ,
,
![]() ,
,
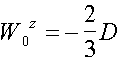 ,
,
![]() ,
,
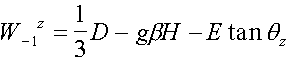 ,
,
![]() ,
(8)
,
(8)
Where 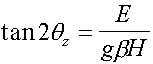 .
.
For
major fields î, ![]() And
And ![]() .
The levels of an energy are submitted on Fig.1:
.
The levels of an energy are submitted on Fig.1:
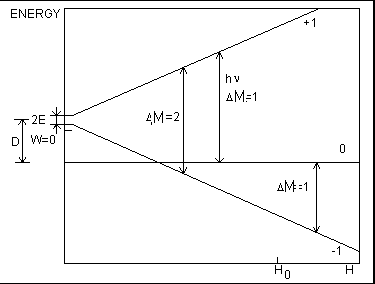
Fig.1
Practically, the choice of axeses is certainly arbitrary. However magnitudes D and å vary thus [8]. The parameters circumscribing an energy distribution in lack of an external field are showed on Fig.1; these levels are gained, if in (5) to take coefficients with opposite is familiar. To each level of an energy of a zero field there corresponds a principal coordinate axis. At a field î, which is parallel to this axes, at magnification of a field the energy does not vary. D is a variance between a level z and two by others. Last are decomposed on 2å. As the sign å can vary at a modification of axeses x and y, we can assume, that both parameters of a zero field are positive. When all three axeses independent, we shall arrange them so, that D> 3å. If two axeses are equivalent, the third direction we shall select for an axes z and å = 0.
Though the dipole - dipole interaction of unpaired electrons are usually comparable to microwave quantum of an energy, it is convenient to consider a case, when the parameters of a zero field are considered as small perturbation. The principal singularities of the shape of a line are taken into account by this approximation. Neglecting D and å, and guessing the g-factor isotropic, and eigenvalues for (7) equal + gbH, -gbH, 0, for spin parts of the eigenvectors we have:
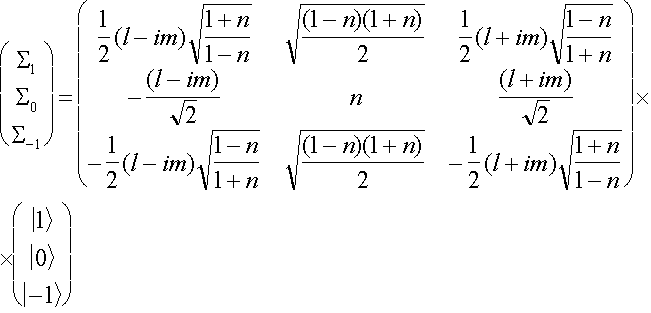 (9)
(9)
[5].
Introducing D and å as perturbation, the levels of an energy in the first order of an approximation will be:
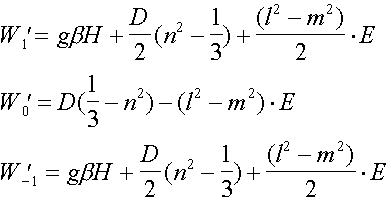 (10)
(10)
With an oscillating magnetic field î1 of ^ î, the transmits 0 - 1 and -1 - 0 are solved. As microwave frequency of oscillations is constant, shall note field, at which is carried out passage as:
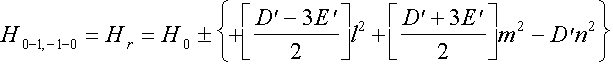 (11)
(11)
Where
the resonance for isolated doublets exists at H0 = hn/geb and D ? = D/geb.
At î to parallel magnetic axeses x, y or z the absorption will be carried
out at îr = H0 £ (D ? - 3E ?) /2, £ (D ? + 3E ?) /2, - (£D ?) in this approximation.
It is axial resonance fields. The lines of transmits DM = 2 with | -1>
on | + 1> are not displaced rather î0. Their disposition is less sensitive
parameters of a zero field, than for transmits with DM = 1. The intensity
of passages with DM = 2 is the second order on D and å2 [5].
At
an evaluation of the shape of a line I (H) in the first order of an approximation
we shall neglect any modifications of a transition probability in field
circumscribed (11). By broaderings of a line as while neglecting, we have
å = 0
If axes x and y are equivalent, (11) passes in:
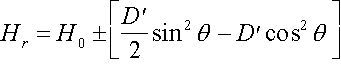 (12)
(12)
Fig.2
In an approximation of point dipoles the following associations [2,9] are valid:
![]() (13)
(13)
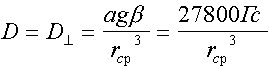 (14)
(14)
Where Dvis - observable decomposition of a doublet of a radical pair with a defined value q; rÓÒ - medial reference distance between unpaired electrons expressed in And; and = 3/2 in (14) corresponds to a case of resonance spins having practically conterminous Larmor frequencies [2].
The improved method of definition of magnitude D from spectrums EPR of radical pairs was offered in operation [10]:
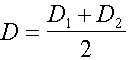 (15)
(15)
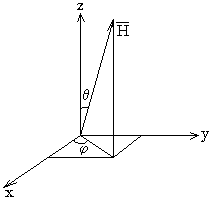
In a coordinate system, figured on Fig.3 the unit vector, directed along a field î expresses by the formula [16]:
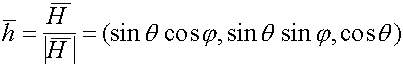 (16)
(16)
If we take into account an anisotropy of the g-factor and å, in limits of our model the spin Hamiltonian gains an aspect:
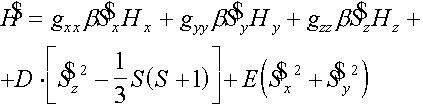 (17)
(17)
Where S - complete spin of a system, the tensors g and d have only nonzero diaganal devices:
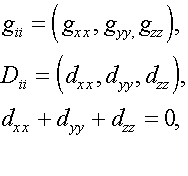 (18)
(18)
And [16]
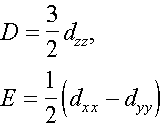 (19)
(19)
In the mentioned above spherical coordinate system, introducing a label
![]() (20)
(20)
Easily we obtain
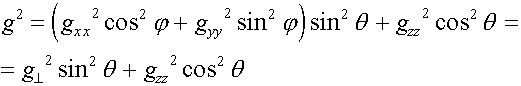 (21)
(21)
If
we take into account only Zeeman interaction, the common solution of a
spin Hamiltonian: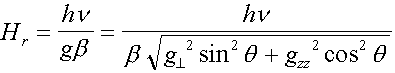 (22)
(22)
That is, according to our model, the position of a line EPR depends on both angles q and j, and, in principal orientations, when the field is guided along axeses x, y, z, the magnitude g makes g = (gx, gy, gz). The extreme positions of an absorption line answer minimum and maximum of magnitudes (gx, gy, gz), and the third g-factor corresponds to orientation of a field, perpendicular first to two. A mode of definition of components of a g-tensor from angular association of spectrums EPR of a monocrystal [16] from here follows.
If except for Zeeman interaction to take into account initial decomposition, for a case S = 1 is obtained
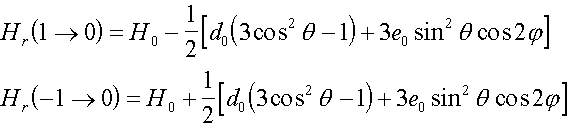 (23)
(23)
Where
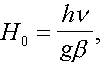
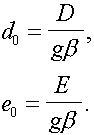 (23Á)
(23Á)
Thus each principal orientation is answered by two lines
H ??
z: ![]()
H ??
x: 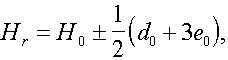
![]() H ?? y:
H ?? y: 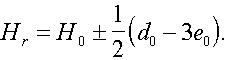
In operation [1] the following formula for definition of common number of spins (that is intensity) in a radical pair is given:
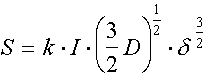 (24)
(24)
Where I and d - amplitude and visual breadth of a perpendicular component, D - magnitude the initial dipole - dipole of decomposition, k - coefficient which is taking into account the shape of a line. For the Gaussian shape of a line k = 1.2, for the Lorentzian shape of an individual line k = 2.
As displays the simple analysis [1], in a case D < 0 lines a, b/ correspond(meet) to passage of a spin from a level M = 0 on a level M = + 1; in case D < 0 the inverse pattern is observed. The usual experimental methods EPR of a spectroscopy allow to find only absolute value, but not signs D [11,12]. Between that the sign D is rather essential to interpretation of outcomes. In an approximation of point dipoles (or noninteracting electrons, field of which delocalization it is a lot of less than distance between radicals) from (2) and (3) follows, that D < 0 and, in this case on magnitude D it is possible to define medial reference distance between unpaired electrons from the formula (14). If D> 0, such interpretation is untrue and, in this case it is possible to speak about a strongly interacting and overlapped spatially two-electronic system [13,14,15].
T he
sign D can be exhibited in spectrums EPR of radical pairs, if the spin
levels are populated nonuniformly, that is factor Boltzman 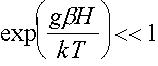 (here î - constant magnetic field, k - constant of Boltzman, ô - Kelvin
temperature) and the electronic spins are polarized (oriented mainly along
a direction of a field). Then the relation of intensities of canonical
peaks in a spectrum will vary, that is the spectrum will become asymmetric
with is familiar to asymmetry depending from D. This case is submitted
on Fig.4; the spectrum (Á) corresponds D>0, and spectrum (Â) D<0. In
usually used EPR 3-ÓÍ of a gamut î ? 3þ103Gs and for observation of polarization
it is necessary to cool a sample up to ô < 0.4K. Probably, just for
this reason effects of soft polarization and the signs D in radical pairs
till now never studied. At using EPR 2-mm of a gamut î ? 5þ104çó necessary
temperature reaches ô < 6.5K. The experiments in such field of temperatures
are quite accessible. Stable radical pairs which are generatrix at a share
attrition of rigid dusts of donor-acceptor junctions (spatially shielded
Fenols and Hinons) [13,14,15] for the first time were in a similar way
examined. The spectrums EPR had the shape figured in the fig. 4Á, that
is for similar pairs D>0. It has allowed to make an output about a strong
coupling of electronic systems of two radicals [13,14,15].
(here î - constant magnetic field, k - constant of Boltzman, ô - Kelvin
temperature) and the electronic spins are polarized (oriented mainly along
a direction of a field). Then the relation of intensities of canonical
peaks in a spectrum will vary, that is the spectrum will become asymmetric
with is familiar to asymmetry depending from D. This case is submitted
on Fig.4; the spectrum (Á) corresponds D>0, and spectrum (Â) D<0. In
usually used EPR 3-ÓÍ of a gamut î ? 3þ103Gs and for observation of polarization
it is necessary to cool a sample up to ô < 0.4K. Probably, just for
this reason effects of soft polarization and the signs D in radical pairs
till now never studied. At using EPR 2-mm of a gamut î ? 5þ104çó necessary
temperature reaches ô < 6.5K. The experiments in such field of temperatures
are quite accessible. Stable radical pairs which are generatrix at a share
attrition of rigid dusts of donor-acceptor junctions (spatially shielded
Fenols and Hinons) [13,14,15] for the first time were in a similar way
examined. The spectrums EPR had the shape figured in the fig. 4Á, that
is for similar pairs D>0. It has allowed to make an output about a strong
coupling of electronic systems of two radicals [13,14,15].
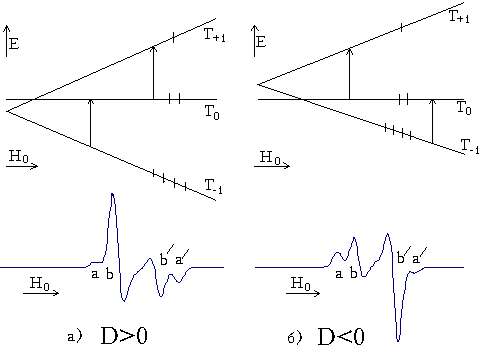
Fig.4